Hi! My 4th semester has just started, so I’m trying to type out as many articles ahead of time so that I don’t have to keep my large (and partially imaginary) audience waiting. (Shh)

Alright, so let’s discuss Tries briefly. This article will mainly give you an overview of what tries are, what they can do, why they’re used, and why you should consider picking them up.

Why learn tries? Tries are very useful in searching for a given string in a set of strings. Now, that’s just the tip of the iceberg but deeper applications of tries may warrant a separate article of its own for another time.

The point here is, tries are efficient, because unlike a naive algorithm to check if a given string exists among n other such strings (which would have a time complexity of O (mn), where m is the length of the search pattern), a trie can determine the presence of a pattern of length m in a set of n strings in O(m). Yeah, proportional to just the length of the pattern.

Let's get formal!

Mathematically, a trie is a classic example of a deterministic finite automaton. Fancy words, I agree, let’s break this down.

An automaton is a machine that has clearly defined states or ‘moments’ during execution, with transitions or connections between these states. (Think of it a lot like a flowchart, if you still find this definition vague)

A transition is made from one state to a connected state upon the corresponding transition character occurring next.

An automaton is called “finite” in nature, when there are a limited number of such states. And a finite automaton is deterministic, when there’s strictly one possible route between two states for a given transition character.



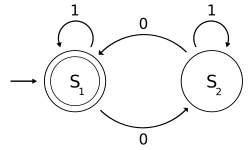
(An example of a DFA, where transitions occur only when zeroes are fed into the states.)

So now that you have a broad idea on what a DFA is, I’ll make my next leap in statements – A trie is a deterministic finite automaton, where each state refers to some substring of some string present in the set of strings.

Additionally, a DFA has an (or more than one) ‘end’ state and in the case of a trie, the last character of a string is the end state of that string.

Basically, what that means, is this -

This is a pretty good representation of how I picture a trie. Basically, in the given image, picture each node as a state, and to transition from one state to the next, the transition variable is the character on the next node.

This means, to transition from the START state to the “A” state, I must input an ‘A’ character and then my machine will undergo the corresponding transition.

Thus, you can see that as I parse the rest of my pattern string, I will have four cases -

• I reach a leaf node after completely parsing my pattern -- implying there's an exact match and the pattern string exists in the source set of strings.
• I reach a leaf node before completely parsing my pattern -- implying my pattern string is a longer string than what's already present in my source set of strings. (For example, what happens, if I try searching for "DOTTED" in the above picture)
• I do not reach a leaf node after completely parsing my pattern -- implying I'm searching for a pattern which doesn't occur separately and at best is a substring of a string that is in my source set. (Try searching for "NO" in the above trie)
• I find no suitable transition as no such connection exists. (For example, try "EAT")

Now, of course, you can implement the dynamic, pointer-based tree structure too but I particularly like the following two-dimensional array based static implementation of the data structure because of its short size (~20 lines, both inserting and querying)

So let’s get started!

The Implementation

Okay, so tries have two functions -

insert( ) - The insert function is invoked when you’re creating the trie and inserting the strings of your source set into the trie, and creating the states and transitions.

find( ) - The find function is invoked when you’ve created your trie and are now checking if a given string is present in your source set or not by transitioning through your trie and effectively thus, checking your source set.

insert( )

//Firstly, the relevant variables -
//Store the transitions for a given state and character
int trie[26][1000];

//A boolean array to tell us if a state has been initialized or not
bool created[1000];

//An array to tell us if a given state is an end state or not
int end[1000];

//To track the newest state
int sz=0;

//Function to insert a string <i>s </i>into the trie
int insert(string s){
     //Initial state of trie
     int v=0; 
     
     //Iterating over the parameter string
     for(int i=0;i < s.length();i++){
          
          //Identifying the transition variable
          int c=s[i]-'a'; 

          //If the state is not yet created
          if(!created[trie[c][v]]){

               //Create it and label it the newest state
               trie[c][v]=++sz; 
         
               //Update the corresponding <i>created </i>hash table
               created[sz]=true; 
          } 
 
          //Transition to the next appropriate state
          v=trie[c][v]; 
     } 

     //Mark the end state as valid
     end[v]++;
}

And that’s how insert works. The reason we took the trie[ ][ ] array to be a 26x1000 array is because there are 26 characters we are considering and we are assuming the maximum number of nodes is 1000, (a reasonable assumption as most problem statements specify the maximum number of characters which in the worst case equals the maximum number of nodes).

find( )

The find( ) function traverses the trie with a given string and checks if the given string is in the trie or not. Here’s how it goes -

int find(string s){

     //Define initial state of trie
     int v=0;

     //Iterate over given string
     for(int i=0;i < s.length();i++){

          if(!created[s[i]-'a'])
            return false;
          v=trie[s[i]-'a'][v];
     }
     return end[v]>0;
}

And that, is how you implement the find( ) method to check whether a given string is present in a set of strings.

The first time I came across tries was in a very straightforward problem on a CodeChef Long Challenge - Blocked Websites (WSITES01), and after the contest upon reading the editorial, did I discover this cool data structure.

Anywho, I just churned out 1k words on this, and now imma hit the bed. Ciao.

Aditya