Minimal Excludants, Partisan games, Impartial games, Sprague-Grundy Theorem, Nim game, Combinatorial Game Theory, Minimax algorithms, and Grundy Numbers.

All of ‘em represent a field of mathematics and computer science, titled “Game Theory”.

(No, not the Economics - Nobel Prize - A Beautiful Mind - Russel Crowe movie but a different “Combinatorial” Game Theory.)

Let’s just jump in!

Firstly, let’s discuss games. Not the console/PC type (PC Master Race <3 tho), but let’s discuss the board games type.

Consider the Nim Game.

The rules are as follows -

• There are 'n' piles of stones in front of you and your opponent.
• The person whose move it is, has the right to choose any pile of stones.
• After choosing a pile, this person may remove any number (>=1) of stones from the pile.
• The last person to make a move (i.e. Remove stone(s) from the final pile) wins.
• In other words, the first person who can't make a move loses.

Such games are called as Impartial Games, games where there is no partiality or bias toward either players. A game where all the information is evident and present to all participants of the game, unlike a game such as Poker or Blackjack.

The concept of Game Theory, mex, and grundy numbers apply only to such full information state games.

Here’s a simulation of Nim Game. Consider 3 piles, each pile having 3, 4 and 5 stones respectively, and A & B are playing against one another.



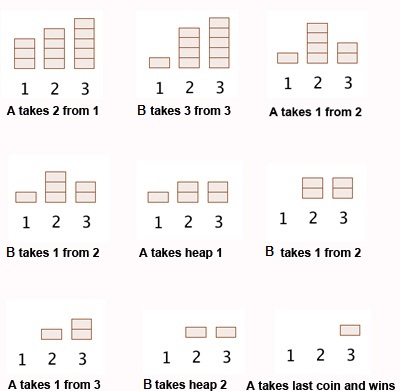
(Note: A started the match in the above simulation)

The fact that all the information is open to both players raises the question – Is it possible to leverage this and make an educated first move? Can the outcome of the game be decided before it even begins? Is that even possible?

Sounds too anime-ish, I agree.

Yes.

Maximum anime cliche achieved.

Consider this alternate scenario where B played first -



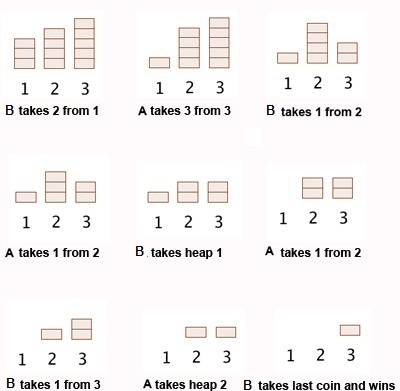
B won. Coincidentally here too, B made the first move.

So does this mean, the starting player unconditionally wins? Can we generalize this observation to that extent?

As it turns out, to a certain degree, yep. The starting player has the upper hand. By that, what I mean is that, he can control the outcome if he plays without making an error.

Here’s the trick to the Nim Game. The cumulative “nim-sum” must be zero.”

The nim-sum operation (more commonly known as the XOR operator), is the key to breaking this game.

There are two observations to be made here -

• Any move made from a losing state, HAS to lead to a winning state. i.e. - notice that any move can only change one of the A[i]. If you change a single bit in an XOR of bits, you will change the final result. So if you start with an XOR total of 0, you must end up with an XOR total of that is unequal to 0.

• There exists SOME move that can bring a winning state into a losing state. i.e. - Find the cumulative XOR of number of stones across all piles, this value has to be lesser than or equal to the number of stones in the largest pile. Thus, the same amount of stones can be removed from the largest pile to lead to a losing state as the other player now has to make a move in a game where the cumulative nim-sum is 0.

The reason XOR, fits in so brilliantly is because of such desirable properties which support our observations.

Thus the key to Nim Game is -

If the cumulative XOR across the board is equal to zero, the player whose turn it is loses. If the cumulative XOR across the board is NON-zero, the player making the turn is guaranteed to win if he plays optimally.

An easy way to understand and even visualize this for faster future recall, is to consider this example, you and I playing this game with 2 piles, of the same number of stones. Say you start, my strategy would be to precisely mirror your move on the other pile. You’ll realize, this way, I’ll always end up making the last move, as you started.

Frankly, up until now before I researched more of Game Theory and Theorems and current algorithms and approaches in the field, this was my primary method of solving. Identify some potential parameters that may play a role in changing the state from a winning to a losing state or vice versa, and then analyse deeply to observe what is the “equivalent number” I need to cumulative XOR over, or perform another such relevant operation on.

Of course, this has its limitations but my success with it gives me some solace in considering it as my last resort.

Coming up next - Grundy Numbers and Mex

This is a number that can define the state of the game.

For example, in the nim game, the grundy number was the stones in a pile (A[i]). Grundy numbers are the numbers associated with the Sprague-Grundy Theorem.

Next post, we’ll be dealing with them and their prerequisite – mex, short for “Minimal Excludant”.

I hope you enjoyed the post, and stick around for part 2 of Game Theory.

Aditya Ramesh