Dynamic Programming: Sum Over Subset
Back! Finally! Things got real, real busy. Ah the hectic life I tell ya.</em>
Anywho, ‘nuff stalling.
So I discovered this neat algorithm a couple of weeks ago while reading the editorial to the problem CODECHEF - MAXOR, and during the contest, I just implemented the brute-force for a quick 20 pts, but couldn’t figure out the 100pt algorithm in time and that’s the inspiration for this article here, and so is this codeforces blog article. Dynamic Programming, mixed in with bit masking, what could go wrong? :)
Let’s dive in!
Basics of bits
x « y : Shifts x by y bits to the left.
x & (1 « y) : Checks if the yth left bit is set in x or not.
x l (1 < < y) : Sets the yth left bit in x.
x ^ (1 « y) : Flips the yth left bit in x.
Incorporating DP
Okay, so consider the following question -
Given a fixed array A of n integers, we need to calculate ∀ x function F(x) = Sum of all A[i] such that x&i = i, i.e., i is a subset of x.
Now, effectively what the question asks of you is to find the sum of all values consisting of pairs where one of the numbers is an entire subset of the other number, in terms of set bits.
To use this method, initially add zeroes to the given array of n integers to get the size to a power of 2. Call this 2^N, with N being the power. The following applies after.
In order to do this, we use a dp array where dp[i][j] stores the answer across all values in A until the (j+1)th bit from the right in all numbers.
The flowchart below, each non-leaf node is of the form (binary, bit index from right considered) that makes the visualization of the data easier.
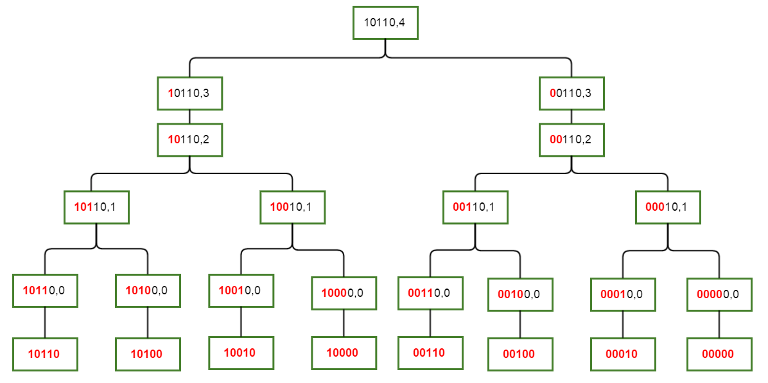
That is, dp[mask][i] would store the result for the sum of all numbers up till bit number i from the right as obtained using mask as a bitmask.
Thus, corresponding dp indices will only be matched when the ith bit is set in mask, where mask iterates over all possible numbers that can be formed (0 to 1«20) in the case of standard problems.
Thus the implementation is as follows -
for(int mask = 0; mask < (1 << N); ++mask){
dp[mask][-1] = A[mask]; //handle base case separately (leaf states)</span>
for(int i = 0;i < N; ++i){
if(mask & (1<<i))
dp[mask][i] = dp[mask][i-1] + dp[mask^(1<<i)][i-1];
else
dp[mask][i] = dp[mask][i-1];
}
F[mask] = dp[mask][N-1];
}
Now let’s explain the code -
Firstly, we handle the leaf states where dp[x][-1]=A[x], as there is no change between dp and A. Having done this, we go to the next step. Iterating over the other bits of the given array of numbers.
The idea of the if case here, is that if mask & (1«i) == 1, then that means the ith bit is set in mask, meaning this value could contribute to the current mask as well, and thus the sum increases and dp[mask][i] is incremented by the value in the mask with the ith bit turned off.
Thus –
If the ith bit is set, the value of dp[mask][i] must consider both, dp[mask][i] AND dp[mask ^ (1«i)][i], the state wherein the ith bit is NOT set.
Else, if the ith bit is off here, one can NOT add the value where the ith bit is on, as then it would no longer store a subset.
To summarize:

The above recurrence, upon further analysis can be space-wise optimized into the following snippet:
for(int i=0;i<(1<<N);i++)new[i]=A[i];
for(int i=0;i<N;i++)
for(int mask=0;mask<(1<<N);mask++)
if(mask&(1<<i))
new[mask]+=new[mask^(1<<i)];
Personally, the hardest part of understanding this is understanding the flow of the code, that is, how the flowchart is filled and the intuitive proof that the subcases have already been solved for through the iterative procedure. Anyway, grasping this was satisfying.
And that’s that!
I may add in an explanation to MAXOR later on, too, but that’s if I find the time to do so, ‘cause I’m swamped with assignments, projects and college work.
Oh well, until next time!
Aditya
