Alright! So, in competitive programming, a powerful data structure exists, called Segment Tree (SegTree)

It’s used primarily to optimize range queries from O(n) to O(logn) where ‘n’ refers to the number of elements.

Consider this example -

You are given an array A of N numbers. You are also given Q queries. Each query is of the form “L R” (without quotes) and you are required to return the sum of the values from index L to index R.

Now, the brute force technique is a matter of implementation. But a segment tree can also be used here. Another common problem is the RMQ problem (Range Minimum Query) where you’re required to find the minimum value between a given L and R index.

Okay, so now the motivation to learn it is clear. Segment Trees are binary trees, as the name implies, and the special property of a segment tree, what makes it so powerful is -

Each node stores the result of its children

In one line, that’s it. That’s the big deal.

Let’s solve the range-sum query problem (given above in italics)

Here, the leaf nodes of the segTree will be the corresponding values in the given array. 

Now, the recursive implementation of segTrees requires 4N space. Its construction takes O(nlogn) as each element is accessed once and for each element, the depth of the tree is traversed.

Consider the array A = {5, 3, 1, 8, 6, 7, 21, 9}



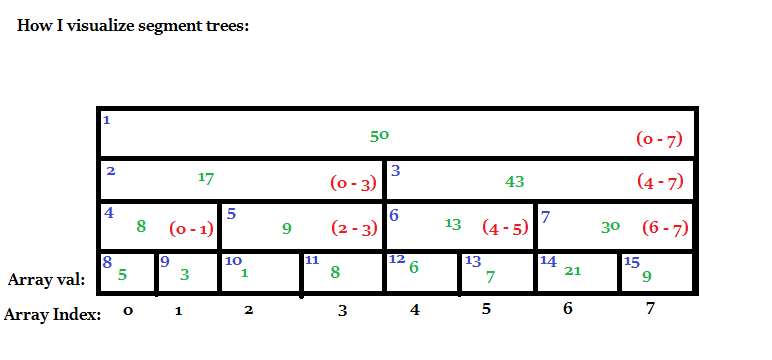
In the diagram, the green numbers are the values on the segTree, the blue numbers are the indices of the segTree (For convenience’s sake, use 1-based indexing as the children of node x are 2x and 2x+1), the red hyphenated numbers represent the range of the pre-processed solution (referred to as node range)

Therefore, building this would be the following way -

    int build(int node,int start,int end){
        if(start==end)tree[node]=A[start];
            else{
                int mid=(start+end)>>1;
                build(node<<1,start,mid);
                build(node<<1|1,mid+1,end);
                tree[node]=tree[node<<1]+tree[node<<1|1];
              }
}

Once you’ve understood that, read this next bit.

The way the segTree works is that once you’re given a query, it repeatedly splits the query into ranges it may have preprocessed for, and once the node range is a subset of the query range, it returns the value at that node. Else it again branches down into both children.

So let us consider three types of overlap:

• No overlap
• Total overlap
• Partial overlap

No overlap - The node range is outside the query range. Thus, you’re looking at a useless node here. Nothing to do, move on.

Total overlap - The node range is entirely inside the query range. This is a completely valid node and a very useful one. Return the value in this node.

Partial overlap - A part of this node range belongs the query range, therefore recurse on both children until there is “no overlap” or “total overlap”.

That’s the query algorithm.

It’s implementation would go as follows -

(Note: start and end here refer to the node ranges, while l and r correspond to the query range.)

int query(int node,int start,int end,int l,int r){
 //No overlap  
  if(l>end || r<start)return 0;
 //Total overlap
  if(l<=start && end<=r)
   return tree[node];         
 //Partial overlap      
  else{         
   int mid=(start+end)>>1;
   int a=query(node<<1,start,mid,l,r);
   int b=query(node<<1|1,mid+1,end,l,r);
   return a+b;
  }
 } 

and that is how the query algorithm is implemented.

 

One of my favorite questions on SegTrees is - Chef and Sub Array

A brute force would fetch 30 points, but a SegTree will fetch 100 points.

Now consider an addition to the question. Assume we were also required to update the value of an index ‘idx’ of A by a value ‘val’. Then, you’d have to implement a point-update method.

This point-update method would be very similar to the build method. The primary difference being – the partial overlap case would have to be modified to invoke the recursive function only if idx lies between start and end (as you’re trying to find that index to update), and when the base case is reached, A[idx]+=val; and tree[node]+=val; 

Due to the recursive nature of the function, all parents of the updated node will also update themselves.

It’s implementation would be as follows -

int update(int node, int start, int end, int val, int idx){
        if(start==end){
                tree[node]+=val;
                A[idx]+=val;
         }
         else{
                int mid=(start+end)>>1;
                if(start<=idx && idx<=mid)
                        update(node<<1,start,mid,val,idx);
                else
                        update(node<<1|1,mid+1,end,val,idx);
                tree[node]=tree[2*node]+tree[2*node+1];
         }
}

Update complexity is also O(logn) as the depth of the tree has to be traversed.

However if a range-update is needed, the point-update method’s worst case complexity devolves to O(n * logn), which must be solved using another technique termed “Lazy Propagation”, which you will find explained in-depth here. :)

In my experience, segment trees are a potential solution when range queries-updates need to be performed optimally, and even more so when a function is commutative and associative. Anywho, I hope this tutorial on segment trees was educational. Feel free to ping me with any comments!

Aditya Ramesh